ソフトウェア技術者のための電子回路 再学習: キルヒホッフの第二法則

キルヒホッフの第二法則も直感で理解できます。

「電気回路網で"任意"の閉路を取り閉路に沿った各素子の

電圧Viの総和は０である」

要するに閉路をぐるっと回ってくると元の電圧に戻るよという意味です。

         

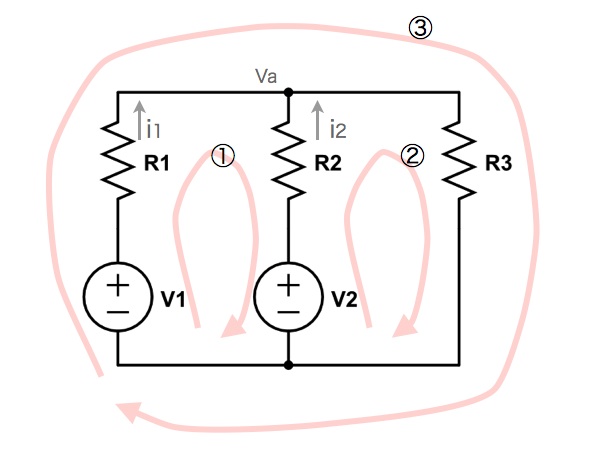
仮に今、上記のような電気回路網があって、"定常状態"の時、ループ①、ループ②、ループ③すべてにおいて、一周回って計算した時に電圧の総和が０になります。

 （電圧の向きに注意）

ループ①　　V1 - R1 x i1  + R2 x i2 -V2 = 0

ループ②        V2 - R2 x i2  - R3 x (i1 + i2) = 0    (キルヒホッフの第一法則よりR3の電流= i1+i2)

ループ③        V1 -R1 x i1  - R3 x (i1 + i2) = 0    (同上)

電池と抵抗でできた回路網の場合、キルヒホッフの第一法則と第二法則で"定常状態の"各点における電圧と電流を求めることができます。

電圧という言葉は、電流を流そうとする圧力のことで、本来ならば回路網の中のある２点を指定して"このポイントとこのポイントの電圧(=電位差)が**V"というのが正確な使い方です。

ただし、実際の電気回路にはグラウンドと呼ばれるポイントが少なくともひとつ以上あるのが普通で、そこを０Vとして、ある一つのポイントが**Vという言い方をすることもよくあります。

回路図をみると以下のような記号が一つ以上含まれているのが普通です。

     　（この二つの記号は同じ意味です)

ここを０Vと考えます。

複雑な回路図になるとグラウンド記号が沢山含まれているのが普通です。

その時、このグラウンド記号は全てつながっています。ですので、回路図をぱっと見た時につながっている部分以外に、くるっとつながっている”回路"が存在していることを頭の中で理解する必要があります。

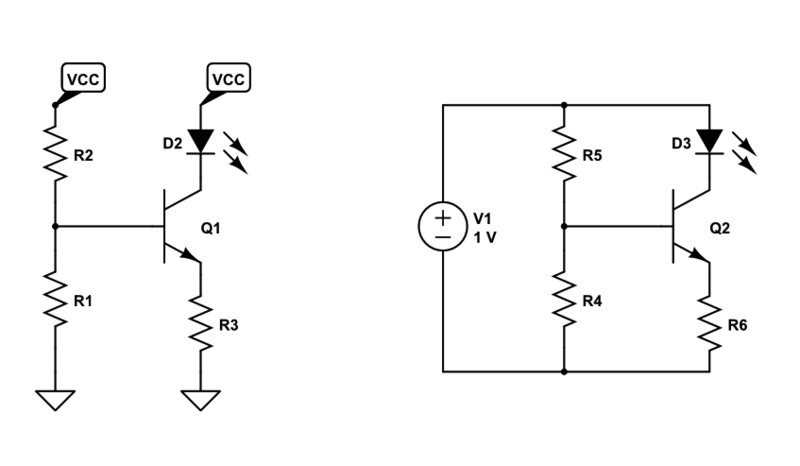
 左のような回路図は実際には右側のような回路網であり、この回路網の中で電流の変化や電圧の変化が起きて、何らかの回路の動作の意味をもっていることを理解する必要があります。

時間的な変化にも様々な種類があって、ある定常状態から別の定常状態に変化することに意味がある回路の場合は(例えばスイッチのON-OFFで状態を変える回路)、キルヒホッフの法則を二つの回路網(スイッチONの回路網とスイッチOFFの回路網)に適用して動作を理解します。

以前に説明したように、正弦波の変化に意味があるような回路の場合はキルヒホッフの法則で定常状態の各点の電流や電位を求めた上でどのような変化があるかを考えます。