JPEGのハフマン符号 (2) AC成分
次にAC成分です。同様にエンコード時を考えます。
AC成分もDC成分と同様に、数値を表現するのに必要なビット数毎にハフマンコードを割り当てて、その直後に数値を記録するという考え方を用います。しかし、さらにランレングス圧縮という手法を組み合わせます。
ランレングス圧縮というのは非常に単純な圧縮法で、同じ記号が続いたら記号と続いた数を記録するという方法です。
Wikipediaのページに説明があります(連長圧縮とも呼ばれます)。
Wikipediaの例にならうと、
A A A A A B B B B B B B B B A A A
という文は以下のように表現できます。
A 5 B 9 A 3
これでかなりの量が圧縮されています。ただし、ランレングス圧縮は常に圧縮できる訳ではなく、データによっては膨らんでしまいます。JPEGでは、AC成分のデータをうまく処理することにより、0の連続値が多くでるような処理を行っています。
以下にある8x8のデータにDCT演算を行った例を示します。
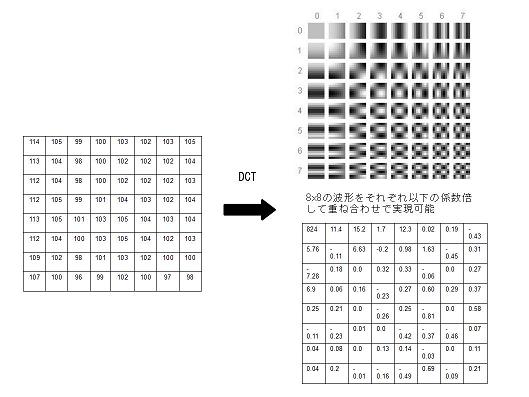
右上の64個の波形をどのように重ね合わせて元のデータを再現できるかを示す値が算出されます(右下の8x8の値)。
JPEGでは、これらの値を量子化係数と呼ばれるもので割ります。

デコードするときは、この係数を掛けて元に戻しますが、その時に丸められた部分の情報は抜け落ちることになります。よって、量子化操作は、右下の周波数の高い波形に対して荒くデータを丸めることを意味します。
人間の目には高周波成分を認識しずらいという性質がありますので、この丸めは問題になりにくいです。
以下に、先ほどのデータ例に量子化演算を行った結果を示します。

右下の方はほとんど0となっています。多くの画像データでこのようなことが起きます。
このデータの性質を利用して、0がいくつ連続したか & 値を表現するのに必要なビット数はいくつかを組み合わせたもので一つのハフマン符号を割り当て、その直後に値そのものを記録します。
その際、左上から右下に向かってジグザグに値を並べていくことによって0が連続する可能性を高めます。
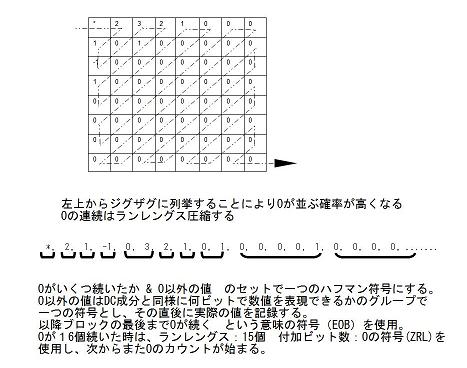
これらの処理により、上記の例では最初のDC成分を除くと、9個の(ハフマン符号+数値)で63個のAC成分を表現できることになります。もちろん丸めでデータが落ちていますが、見事に人間には認識しずらい部分のデータを選択して劣化させていることになります。
以下にハフマン符号表の一例を示します。
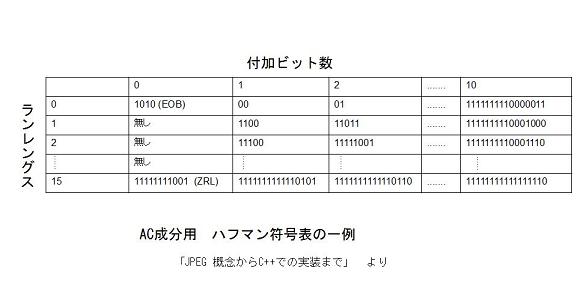
152個の符号がありますが、これはすべて準備する必要があるわけではなく、画像によって使われていないものは無くてもかまいません。また上記は一例ですが、当然その画像データ中で出現確率の高いものに短い符号を割り当てます。
先ほどのデータ例を含むデータをjpegsnoopに掛けてみると以下のようにAC成分用のハフマンテーブルが出力されます。
jpegsnoop出力ファイルjpegsnoopAC.txt
先ほどの例をこのハフマンテーブルによって最終的に圧縮すると以下のようになります(使用しているハフマン符号のみ図に記入しています)。
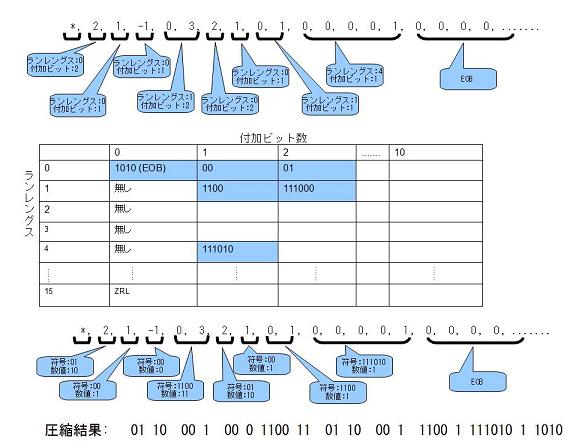
最初の8x8の画像データがかなり少ないビットに圧縮されています。