JPEGのハフマン符号 (1) DC成分
JPEGのハフマン符号を理解するため、エンコード時の符号化を考えます。
JPEGのハフマン符号は、画素の値をそのまま符号化はしません。
・画素の値を表現するために必要なビット数をハフマン符号化してデータ圧縮を行います。
・DCT出力値のAC部分とDC部分で異なる圧縮法を用いて、圧縮効率を上げています。AC部分はランレングス圧縮と言われる方法とハフマン符号化を組み合わせて圧縮効率を上げています。
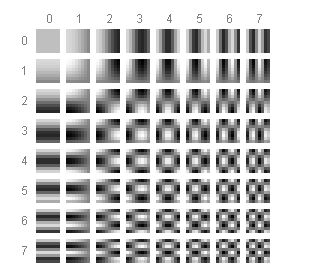
2次元離散コサイン変換は、以下の図のような64個の8x8の離散波形の重ね合わせで元の8x8のデータを表現する正規直交変換です。
フーリエ変換と同じように、上記の64個の波形のセットが、8x8の任意の画像(8x8の離散値を取る1コンポーネントの画像)を表現できる基底関数となります。変換後に出力される8x8の値は、それぞれ図上の波形が何%重ね合わせるかを示す係数となります。値がマイナスの場合は反転します。
ここで、一番左上の升目の波形は8x8全てが同じ値をとる定常波です。ここの値をDC成分と呼びます。残りの63個の値をAC成分と呼びます。JPEGでは、AC成分とDC成分で異なる方法で圧縮します。
このエントリでは、DC成分のハフマン符号化について書きます。
画素の値は-255〜255まで大きな幅があります。これをそのままハフマン符号化すると大変大きなハフマンテーブルが必要になります。またDC成分は8x8ブロック全体のベースとなる値です。画像全体では様々なばらついた値を取る事が予想されます。
ハフマン符号は前回のエントリで見たように、ごく一部のコードの出現確率が高ければ高いほど圧縮効率が高くなります。DC成分は画像全体ではかなりばらばらの値を取ることが予想されますが、隣り合ったブロックでは色調がなだらかに変化する場合が多いので、隣り合ったブロックのDC成分の差は小さな値になる確率が高くなることが容易に予想できます。
そこでDC成分については、値を直接記録するのではなく、一つ前のブロックのDC成分との差を記録することにします。
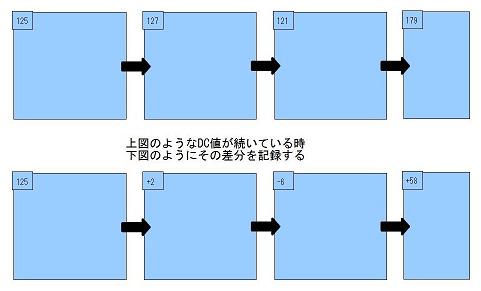
このようにすることで±0近辺の値の出現確率が非常に高くなりますのでハフマン符号化の圧縮効率が高くなります。
このような手法を用いることで存在確率の偏りを作り出すことには成功しますが、画像全体では様々な種類の色調が用いられますので、沢山の種類の数値が記録されます。-256〜+256までの数値にそれぞれ符号をつけていくとハフマンテーブルが非常に大きくなります。また、たまにしか使われない値のコードは非常に長くなってしまいます。
そこでJPEGでは、値そのものをハフマン符号化するのではなく、値を表現するために必要なビット数を符号化して、その直後に値を示すという方法を取ります。
言葉にすると非常に分かりにくいのですが、単純なことです。最初に分かりやすく説明するため、すべての値が正である時について説明します。
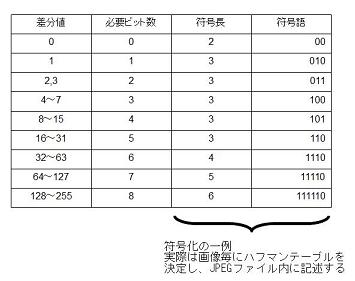
上図は仮のハフマン符号化の符号例です。
例えば 6 という値を符号化するときには、符号語 100 に続けて 6 を意味する2進数 110 を続けて 100110 と記録します。
67 という値を符号化するときには、符号語 11110 に続けて 67 を意味する2進数 1000011 を続けて 111101000011 と記録します。
2進数で数値を表現した時に必要となるビット数でグループ分けし、一つのグループに対して一つのハフマン符号を割り当てているようなイメージです。その符号を解読することにより次の何ビットが実際の数値かを判断して読み込むことによって解読できます。
1を表すグループに値が一つしかないので符号語のみで表現できる等の冗長性があるように感じますが、実際はマイナスの値も表現しますので冗長性はなくなります。
マイナスの値に対しては、1を引いた値に直して符号化します。
以下にマイナスの値まで対応したハフマン符号例を示します。
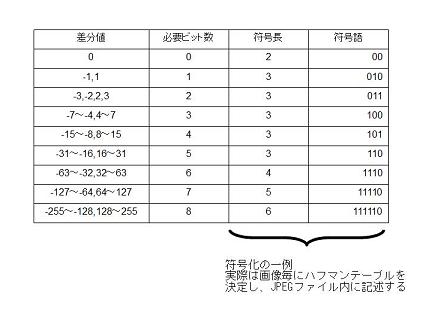
例えば -1 という値を符号化するときには、符号語 010 に続けて -1-1 = -2 を表す2の補数の下位1ビットの 0 を続けて 0100 と記録します。
- 63 という値を符号化するときには、符号語 1110 に続けて -63-1 = -64 を表す2の補数の下位6ビットの 000000 を続けて 1110000000 と記録します。
ここにあげている符号語は一例にすぎません。
ためしに、jpegsnoop にあるjpeg画像を与えてみたところ、一つ目のハフマンテーブル部分の出力は以下のようなものでした。
Destination ID = 0
Class = 0 (DC / Lossless Table)
Codes of length 01 bits (000 total):
Codes of length 02 bits (001 total): 00
Codes of length 03 bits (005 total): 01 02 03 04 05
Codes of length 04 bits (001 total): 06
Codes of length 05 bits (001 total): 07
Codes of length 06 bits (001 total): 08
Codes of length 07 bits (001 total): 09
Codes of length 08 bits (001 total): 0A
Codes of length 09 bits (001 total): 0B
Codes of length 10 bits (000 total):
Codes of length 11 bits (000 total):
Codes of length 12 bits (000 total):
Codes of length 13 bits (000 total):
Codes of length 14 bits (000 total):
Codes of length 15 bits (000 total):
Codes of length 16 bits (000 total):
Total number of codes: 012
Expanded Form of Codes:
Codes of length 02 bits:
00 = 00 (EOB) (Total Len = 2)
Codes of length 03 bits:
010 = 01 (Total Len = 4)
011 = 02 (Total Len = 5)
100 = 03 (Total Len = 6)
101 = 04 (Total Len = 7)
110 = 05 (Total Len = 8)
Codes of length 04 bits:
1110 = 06 (Total Len = 10)
Codes of length 05 bits:
11110 = 07 (Total Len = 12)
Codes of length 06 bits:
111110 = 08 (Total Len = 14)
Codes of length 07 bits:
1111110 = 09 (Total Len = 16)
Codes of length 08 bits:
11111110 = 0A (Total Len = 18)
Codes of length 09 bits:
111111110 = 0B (Total Len = 20)
この例では、3bitのコードが沢山使われています。前回のエントリで書いたように、各符号の出現確率のばらつき方によって最適な符号化が異なります。
また、jpeg規格では、ハフマンテーブルを複数持つことができます。各コンポーネント毎にどのハフマンテーブルを使用するか指定できるのですが、大体において、YでDC,AC用ハフマンテーブル各1つ、CbとCr共通でDC,AC用ハフマンテーブル各一つづつ使っていることが多いようです。
それと、DC成分の差分の計算を途中でリスタートするリスタートマーカーというマーカーが存在します。このマーカーがはいるたびに一つ前のDC値は0にリセットされて計算がはじまります。差分が続くとどこかで一旦間違えたら延々と間違えたままになりますが、このマーカーが入ることで防げます。しかし、ここではリスタートマーカーは扱いません(リスタートマーカーが入った motionJPEGの作成方法がわからないため)。