ハフマン符号のアルゴリズム

非常に簡単にハフマン符号について説明します。

アルゴリズムの教科書は沢山読みましたが、私が最も良いと思ったものは以下のものです。

「アルゴリズムイントロダクション」T.コルメン　C．ライザーソン　R.リベスト　　近代科学社

定評のある本なので良く読み返します。
この中のハフマン符号についての例をそのまま持ってきました。

a,b,c,d,e,f という6種類文字を使用した100000文字の文があるとします。出現頻度の行に書いてある値がそれぞれの文字が全体に対してどれだけの割合があるかという意味です。
6種類の文字は3ビット使用すればすべて表現できます。固定長符号の行にそのコードアサインの一例を示しています。すべての文字に対して3ビット用いるので、3x100000ビットで全体が表現されます。

この他に、文字毎に使用するビット数を変えるコードアサインもあります。可変長符号の行にそのコードアサインの一例を示しています。全体の文を左側から読んでいった時に冗長にならずに、かならずどれか一つのコードにのみ割り当てられるようなコードが用いられています。そのためもっとも少ないビット数は1ですが、最も長いコードは固定長符号よりも大きいビット数を必要とします。
しかし、ここでaの出現頻度は45%もありますので、全体の文中の半分近くが1ビットで表現できることになります。このように出現頻度の高い文字に短いコードを与えれば全体の文を表現するための総ビット数が固定長符号よりも少なくなります。

このような符号は以下のような二進木で表現することができます。

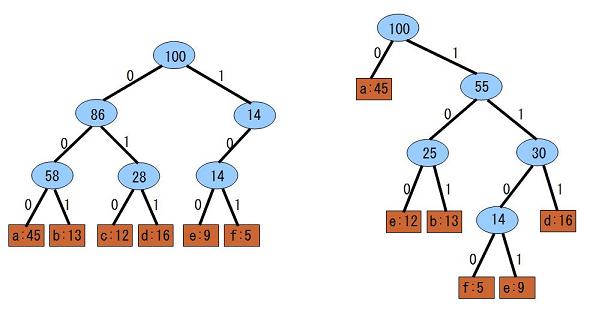
左側が固定長符号を表現した二進木で、右側が可変長符号を表現した二進木です。文から読み込んだビットに従いルートからツリーをたどっていきます。リーフに付いた場合はそのリーフが対応する文字であると解読し、またルートからツリーをたどり始めます。
このようなツリーで表現されるコードであれば、冗長にならずに元の文を復元できることになります。

出現確率が高い文字は少ない段数でリーフにたどり着くようなツリーを構成すれば圧縮効率は高くなります。
例えば二つの文字が文中の殆どを占め、その他の多数の文字がほんの少しだけでてくるような文であれば、ルートから左側に二つのリーフを配置して右側には深い完全二進木となるようなツリーを構成すれば圧縮効率が高くなることは容易に想像できます。

実は出現確率が与えられた場合にもっとも圧縮効率の高くなる二進木を構成する方法はグリーディなアルゴリズムで非常に簡単に構成できます。