データパスのビット長（１）

データパスのビット長を決定しなければなりません。
インターフェース誌の記事を参考に、同じような考察をYCC-RGB変換モジュールのデータパスに対して行ってみます。

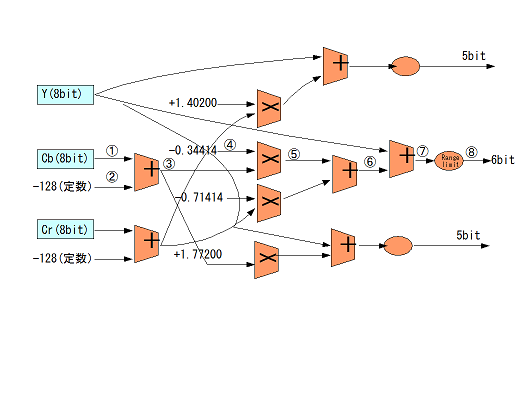
ソフトウェアであれば、INT型、DOUBLE型と演算のビット幅は決められたものから最適なものを選びます。しかし、ハードウェアではその幅は自由に決めることができます。その代わり、データパス部分はハードウェアのリソースをたくさん使いますので、ソフトウェアがINT型で乗算をしているからといって、３２ビットｘ３２ビット演算等を使うと面積的に厳しいことになりますし、データパス部分のクリティカルパスが長くなってしまい、その部分が全体の周波数を押し下げることにもなりかねません。
よってできる限り少ないビット長で演算を行うのが得策ですが、あまりにもビット長を小さくすると、今度は誤差の問題が出てきます。このバランスをとらねばなりません。
今回のデータパスにおいては、Cbと-128の入力から真ん中の6ビット出力の部分がもっとも誤差に対して厳しいパスと考えられます。
理由）
１.　データパスの演算の段数が一番多い。何も考えずに出力ビットすべてを保持していくと出力ビット数は非常に大きくなり無駄になる。
２.　16ビットカラーでは、RGB全てを同じビット数にできないため、どれかのビット数を大きくしている。
人間の目はGREENに対して敏感であるため、Gだけ６ビットとなる。
IJGのJPEG　LIBRARYは３２ビットカラーでR,G,Bすべて８ビット出力だが、今回１６ビットカラーにする際に下位ビットを切り捨てる。R,Bは３ビット切り捨てるが、Gは２ビット切り捨てることになる。
よって、R,BよりもGの方がデータパスのハードウェア演算で許容される誤差が厳しい。

という訳で、図中の真ん中のパスを考察してみます。
まず、入力部分と出力部分で、前後のつながりからビット幅が確定する部分があります。
?Cbは8ビットで入力されますが、これは符号無しの８ビットで0〜255の大きさをとります。最初に符号付の加算があるために、１ビット拡張して９ビットの符号付きの値に変換します。
?も符号付の９ビットで表現して加算します。出力は１０ビットとなりますが、値は-128〜127になりますので、上位２ビットは切り捨てて良いことになります。捨てた部分に関しての加算器の最適化は論理合成ツールにまかせます。これで?は符号付き８ビットとなります。

次に出力部分ですが、図中のRange limitという演算は０以下なら０に固定、255以上なら255に固定という演算です。この値が符号無し８ビットであらわされて、その後下位２ビットを切り捨てて6ビット出力となります。よって?の加算器の出力は、2^3-1(-3〜３）まで誤差があってもまったく影響がないことになります（下位２ビットまでは誤差があっても同じ値になる）。

ここまでが入出力の値の範囲から決定される部分です。この条件の下、乗算のビット数とその後の二つの加算のビット数を決定します。

?を出力として持つ加算器の一方の入力は１ビット符号拡張した９ビットの整数定数であり、誤差は含まれません。よって?の誤差がそのまま?の誤差になりますので、?に許される誤差も２^3-１（-3〜3）となります。
?に許される誤差は加算器の二つの入力誤差の和が出力誤差になりますので、?に許される誤差の二分の一となり、2~2-1(-1〜１）です。
これで?の入力を２進数で小数点以下を何ビットで表現するべきかが決まります。
すでに?は符号付８ビット（-12８〜127）で誤差がない状態に確定しています。
?を小数点以下６ビット持てば、誤差は2^(-7)以下となり、-128〜127の間の数値を乗算しても誤差が-1〜１の間に収まります。整数部分に１ビット、符号部分に１ビット必要ですので、?は符号付８ビット（うち６ビットが少数点以下）に確定しました。これにより乗算器も符号付８ビット２入力に確定です。

符号付８ビット乗算器の出力は１6ビットになります。そのうち６ビットが少数点以下を表します。整数部分は符号付の１０ビットです。ここで先ほど考察した許容誤差を考えると少数点以下の６ビットの出力は捨ててしまって問題ないことが分かります。整数部分の最下位１ビットも捨ててしまい、０に固定します。このようにして乗算器の最適化を論理合成ツールに任せます。乗算器と言っても一方の入力は固定値ですので、通常の符号付８ビット２入力の乗算器よりもかなり小さくなると予想しています。

乗算器の出力の最大値、最小値を考えて見ます。
実は二つの乗算器に入力される定数の絶対値が１以下ですので、可変する側の符号付８ビット入力変数よりも整数部分の絶対値は必ず小さくなります。よって乗算器の整数部分出力ビットも８ビットでよいことになり、２の補数で表しているため上位２ビットも捨ててしまってかまいません。
（ただし、他の二つの乗算器は与えられた定数が１以上２以下ですので、上位１ビットしか捨てることはできません。この二つの乗算器の出力は符号付９ビットを有効にします。）

?が符号付８ビットに切り捨てられましたので、次段の加算器は符号付８ビット２入力となり、出力は符号付９ビットです。そして次の加算器は符号付９ビット２入力となり、出力は符号付１０ビットです。
その後range limitによって情報を削ります。

とりあえず、データパスのビット幅が確定しました。
これであっているかなー？？？

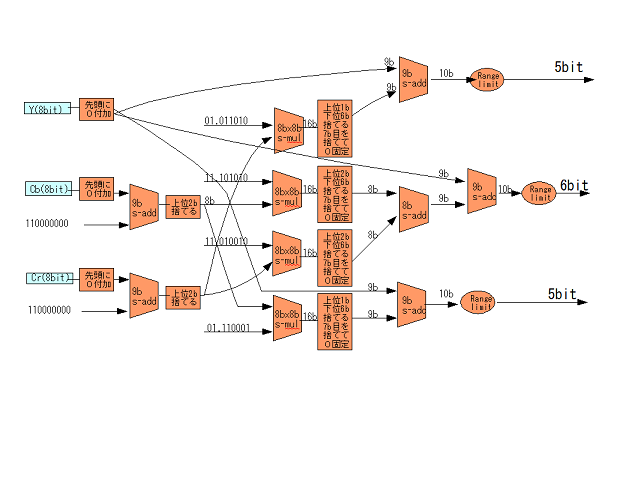
次にこれであっているかソフトウェアで検証するつもりです。
（しかし、この文章じゃ、全然意味が通じない気がします。後でもっとうまく書き直したい。）

後記：
ここまでやっておいて、両方が変数になっている乗算器がひとつもないことに気が付きました。
もしかしたら、最後のRangeLimitのところでビットを捨てて、あとは論理合成ツールにまかせてもほとんど変わらない面積で収まるのではないかということを感じつつあります。。。。。。。
まあ、勉強になったから良いか。

後記2：
ちょっと基本的な考え方を誤解していたみたいです。後で検討しなおします。